
THE BEGINNING OF ALL LAWS
The other day I was reading Leonard Susskind and George Hrabovsky’s ‘Classical Mechanics: The Theoretical Minimum’, and I found in the first interlude something so simple and beautiful- the origin of dynamic laws. I’ll begin by laying down foundations (as I’ve learnt in the book) then picking it up from there.
The purpose of this explanation is to showcase the inherent beauty of dynamical laws and how they can be written down mathematically by using state-spaces.
THE ASSERTIONS
There exists objects. A collection of these objects form a system. A closed system is defined as a set (collection) of objects which operate without consideration to what exists outside it.
What is a set-space? It is a set of all possible states an object may have. Take for instance a coin, which only has two possible states, Heads or Tails.
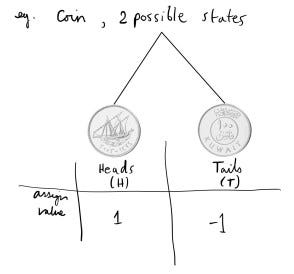
Now this for me is almost comparable to sample spaces (total outcomes) in probability theory. Whereby a coin has only two possible outcomes, Heads or Tails. The difference is however the implied transition of time in the state-space, meanwhile probability is a measure of likelyhood of becoming that state (or outcome).
There are two transitions of time, continuous and discrete. Discrete is countable, eg. 1, 2, 3, … etc. We’ll be denoting discrete time as ‘n’.
Now lets bring back the coin state-space example and assign the value of 1 to Heads and -1 to Tails.
In order to be able to define state changes mathematically we must define them as dynamic. Dynamical systems are systems that change over time.
With the upcoming example dynamical laws we’ll see our objective of converting linguistic descriptions of state changes into mathematical ones.
EXAMPLES OF DYNAMICAL LAWS
Dynamical law #1,
“Whatever the state at time n, the next state is the same”.

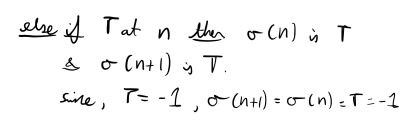
Dynamical law #2,
“Whatever the state is at the instant at time n, the next state is the opposite”.

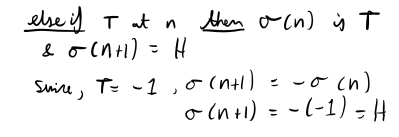
As you can see, both of these assumed laws are deterministic and reversible which are the two conditions necessary to make them valid dynamical laws. A side note, reversible means we can tell the future as well as the past.
Having reached our main objective for this post, converting linguistic to mathematical and showing that the two assumed laws form valid dynamical laws, I am interested in knowing whether the concept of state-spaces has indeed been applied to mathematical finance?
A quick google search yields an answer and hence a subject for my next post.
THE BOOK
I am only halfway through the book and I’m already finding it an awesome eye opening read. It boasts a multitude of examples as well as its extremely well thought out layout. Each idea is introduced with flair. The book helps you brush up on your mathematics and then shows you how the math is applied to physical concepts. If you’re interested in a bottom up approach of understanding classical mechanics this is the book for you!

