
WHAT IS ARBITRAGE
Arbitrage is when the same asset has, for example, two different prices across markets and hence an investor can profit by immediately buying and selling to profit from the price differential.
Suppose a stock A was trading at $100/share at the NYSE and $105/share at the SEHK. Once this price differential is noticed, an investor would buy let’s say 10,000 shares of stock A at the NYSE and immediately sell them to the SEHK. The profit realized would be $5 per share amounting to a total of $50,000 in profit.
Look back at the example and you will be able to deduce that this trade was risk-less, there was a guaranteed profit realized at the end of the trade, and it cost nothing to immediately buy and sell the stock.
With these deductions in mind we can begin to structure the formal definition of arbitrage.
THE FORMAL DEFINITION OF ARBITRAGE
An arbitrage portfolio is one where you pay nothing to enter it, and you make a certain risk-less positive profit.
Mathematically speaking it looks something like this,

The following example is the one I learnt from ‘Financial Derivatives: A Quantitative Finance View’ course on Udemy by Cameron Connell.
THE EXAMPLE
We have 3 stocks: A, B, and C.
The prices of these stocks at time t is:
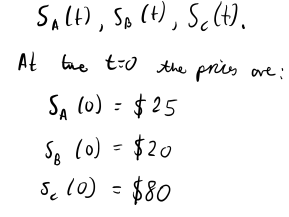
At time t=1 there exists two independent states, state 1 & state 2:

There exists a relationship between the three rows in all states:
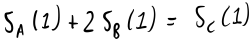
Now apply this relationship to prices at t=0,

With our new found suspicion of an arbitrage, we will construct an arbitrage portfolio and assume that an arbitrage does exist because of this misprice.
Construct the arbitrage portfolio as follows:
At time t = 0, enter the following portfolio:
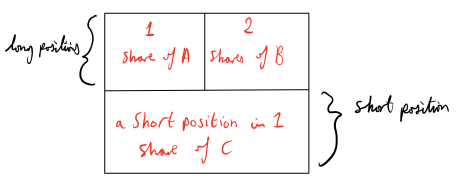
The total cost of entering the long positions is:
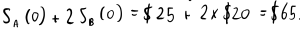
Shorting one share of stock C immediately yields $80, therefore we profit the difference = $15
We hold the positions till t = 1 & in both states we have:
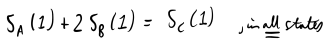
Therefore, in both states we must sell our long positions, buy back one share of C at Sc(1) and return it to its owner to close our short position.
Another assumption is that we left our profit of $15 to grow continuously compounded at a risk-free interest rate r till t=1:

Finally, we can say that the total cost of entering this portfolio was nothing and we made a certain risk-less positive profit of

, hence this is an arbitrage portfolio.
WHY DOES ARBITRAGE HAPPEN?
There are many reasons why arbitrage may happen. However it is important to keep in mind that they occur during short periods of time.
One of the reasons why they happen is due to the unequal distribution of information. This includes delay in relaying price changes. As you can probably guess with the technological advancements we’ve seen it is very difficult to see these delays.
Another reason would be due to inefficient markets. An inefficient market is one where security price changes are random and are independent of historical events. This also carries the implicit economic theory idea where a securities market price does not reflect its true value.
NO SUCH THING AS A FREE LUNCH
The concept of arbitrage in economic theory is regarded as a non-equilibrium phenomenon. Since this phenomenon is shortlived it is regarded as a transient phenomenon.
While the concept does exist in reality, in quantitative finance it is assumed to not exist due to its transient nature. Therefore we regard derivative pricing as an economic equilibrium activity.
Enter the no-arbitrage principle, which coincidentally is our upcoming topic!
